Introduction
Logistic regression is a popularly used model for binary classification tasks, in which the objective is to determine the probability of a binary outcome based on input features. While logistic regression is powerful and interpretable, it can be prone to overfitting, especially when there are many features or highly correlated predictors. Regularisation techniques, such as Lasso (L1 regularisation) and Ridge (L2 regularisation), help address these issues by penalising the complexity of the model. This article will discuss how to fine-tune logistic regression models using these regularisation methods, focusing on their theoretical foundations, differences, and practical implementation. Acquiring in-depth knowledge in this subject is essential for anyone pursuing an advanced-level Data Scientist Course.
The Basics of Logistic Regression
Logistic regression predicts a binary outcome, typically encoded as 0 or 1. It works by estimating the probability of the outcome belonging to class 1 given a set of input features. In its simplest form, logistic regression models the relationship between the dependent variable (the binary outcome) and independent variables (the features) using a logistic function. The output of the logistic function is a probability score that is bounded between 0 and 1, which can then be mapped to a class label (0 or 1).
Despite its simplicity and ease of interpretation, logistic regression can suffer from overfitting when the number of predictors is large or multicollinearity among features. This is particularly problematic in high-dimensional datasets where the model may capture noise, leading to poor generalisation of unseen data. A Data Scientist Course will help you understand how to use techniques like regularisation to overcome such challenges.
Regularisation and Overfitting
To combat overfitting, regularisation techniques penalise the complexity of the model. Regularisation works by adding a penalty term to the model’s cost function, discouraging overly large coefficients for the features. This forces the model to focus on the most important predictors and reduces the risk of overfitting. The two most commonly used regularisation methods are Lasso and Ridge.
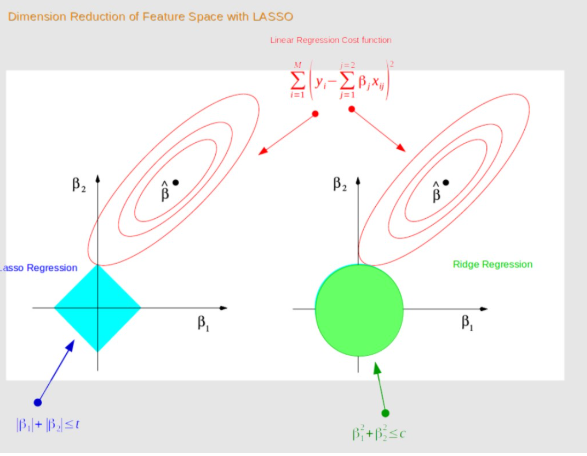
Lasso (L1) Regularisation
Lasso, which stands for Least Absolute Shrinkage and Selection Operator, is a regularisation technique that adds a penalty based on the absolute values of the coefficients in the model. Its key characteristic is its ability to drive some coefficients exactly to zero, effectively eliminating irrelevant or less important features. This makes Lasso particularly useful for feature selection, as it automatically identifies the most relevant predictors and discards the rest.
One of the main advantages of Lasso is that it simplifies the model by reducing the number of predictors. This is particularly beneficial in cases where many features are available, but only a subset of them are contributing to the prediction. However, Lasso can behave unpredictably when the features are highly correlated, as it tends to select only one feature from a group of correlated features and discard the rest. Knowledge of Lasso regularisation is often taught in a Data Scientist Course, as it is a powerful tool for handling high-dimensional datasets.
Ridge (L2) Regularisation
Ridge regularisation, on the other hand, adds a penalty based on the square of the coefficients. Unlike Lasso, Ridge does not shrink coefficients to zero but instead reduces the magnitude of all the coefficients. This results in a more evenly distributed reduction in the model’s complexity. Ridge is especially useful when there is multicollinearity among the features, which occurs when two or more features are highly correlated. By applying Ridge regularisation, we prevent large coefficients for correlated features, which helps stabilise the model and avoid overfitting.
Ridge does not perform feature selection like Lasso, as it does not eliminate any features. Instead, it penalises all coefficients equally, which can be useful in situations where every feature may have some contribution to the outcome. However, Ridge may not perform as well when only a few features are important for prediction, as it does not offer the same sparsity level as Lasso. Understanding these differences between Lasso and Ridge is often part of a comprehensive Data Scientist Course.
Elastic Net Regularisation
Elastic Net is a hybrid regularisation technique that combines the strengths of both Lasso and Ridge. It includes both L1 (Lasso) and L2 (Ridge) penalties in the cost function, making it suitable for situations with many correlated features. Elastic Net allows for both feature selection (through Lasso) and stabilisation of correlated coefficients (through Ridge). It is often the go-to choice when neither Lasso nor Ridge is sufficient on their own.
Fine-tuning the Regularisation Parameter
The key to using Lasso and Ridge effectively lies in selecting the appropriate regularisation strength, typically controlled by a hyperparameter. For both Lasso and Ridge, this hyperparameter is often referred to as λ or CCC (which is the inverse of λ). The goal is to find the optimal value of this hyperparameter that balances the model’s ability to generalise to new data while avoiding overfitting.
Cross-validation is commonly used to tune this parameter. Cross-validation involves splitting the dataset into multiple subsets (or “folds”), training the model on some of the folds while testing it on the remaining fold. This process is repeated for different training and testing data combinations, and the performance is averaged to estimate how well the model generalises. A common technique for selecting the best regularisation parameter is grid search, where a range of possible values for the regularisation strength is tested, and the one that minimises the validation error is chosen.
It is recommended that data professionals seeking to gain the skills to implement and fine-tune logistic regression models with regularisation enrol in a well-rounded advanced-level data course such as a Data Science Course in Mumbai that covers techniques for improving model accuracy and robustness.
Implementing Lasso and Ridge Regularisation in Python
In Python, the scikit-learn library provides straightforward implementations for Lasso and Ridge regularisation. Following is an example of how to fine-tune a logistic regression model using both methods.
Lasso Regularisation (L1)
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import make_classification
# Generate synthetic binary classification dataset
X, y = make_classification(n_samples=100, n_features=20, random_state=42)
# Create Logistic Regression model with Lasso (L1) regularization
lasso_model = LogisticRegression(penalty=’l1′, solver=’liblinear’)
# Define parameter grid for regularization strength (C is the inverse of lambda)
param_grid = {‘C’: [0.001, 0.01, 0.1, 1, 10, 100]}
# Perform grid search with cross-validation
grid_search = GridSearchCV(lasso_model, param_grid, cv=5)
grid_search.fit(X, y)
# Output the best regularization parameter
print(f”Best regularization parameter C: {grid_search.best_params_[‘C’]}”)
Ridge Regularisation (L2)
# Create Logistic Regression model with Ridge (L2) regularization
ridge_model = LogisticRegression(penalty=’l2′, solver=’liblinear’)
# Define parameter grid for regularization strength (C)
param_grid = {‘C’: [0.001, 0.01, 0.1, 1, 10, 100]}
# Perform grid search with cross-validation
grid_search = GridSearchCV(ridge_model, param_grid, cv=5)
grid_search.fit(X, y)
# Output the best regularization parameter
print(f”Best regularization parameter C: {grid_search.best_params_[‘C’]}”)
In both examples, we use the inverse of λ (denoted as CCC) as the hyperparameter to tune. The GridSearchCV function is used to perform cross-validation over a range of possible values for CCC to find the value that minimises the validation error.
Conclusion
Fine-tuning logistic regression models using Lasso and Ridge regularisation is essential for preventing overfitting and improving model performance, particularly in high-dimensional datasets. Lasso excels in feature selection by shrinking some coefficients to zero, while Ridge stabilises the model by reducing the magnitude of coefficients. By tuning the regularisation strength using cross-validation and grid search, it is possible to find the optimal balance between model complexity and generalisation. Whether using Lasso, Ridge, or Elastic Net, regularisation helps ensure the model performs well on the training and unseen data. These fundamental concepts are typically covered in the course curriculum of any advanced-level data course such as a Data Science Course in Mumbai that equips learners with the essential knowledge and tools proficiency for performing real-world data science tasks.
Business name: ExcelR- Data Science, Data Analytics, Business Analytics Course Training Mumbai.
Address: 304, 3rd Floor, Pratibha Building. Three Petrol pump, Lal Bahadur Shastri Rd, opposite Manas Tower, Pakhdi, Thane West, Thane, Maharashtra 400602
Phone: 09108238354
Email: enquiry@excelr.com